When we use explosives, there are two features that military engineers leverage in particular: the blast and brisance. The blast effect is used to “push” and the brisance effect is used to shatter. Blast effects are carried out by the large volume of hot gases that expand out from the explosive so using a large volume of explosive makes a lot of sense for optimal blast.
Brisance is generally understood to be more closely tied to the shock wave. But the emphasis in most people’s understanding is that it is a shock, and the fact that it is a wave is not well leveraged. Specifically, one of the defining features of waves is their ability to constructively and destructively interfere with each other, and this effect can be leveraged to enormous effect with shock waves.
Regular pressure waves are just sound waves, and when you add them up, the resulting pressure is the sum of the sound wave pressures. This is because sound wave occur in the elastic region of the stress-strain curve which is linear; when a molecule is disturbed by a sound wave, it returns to its original state as if it was attached to a nice little spring.
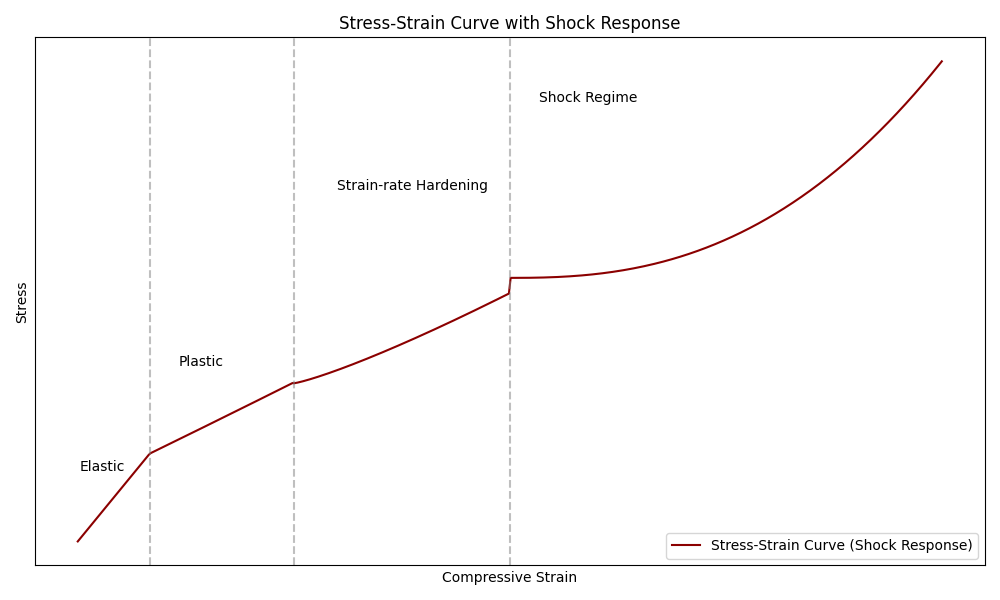
Shock waves are not so linear. When a shock wave travels through a material, the compression is so high that the material acts more like a fluid being deformed like plasticine. The molecules are therefore not bouncing back to where they were as if attached to little springs. This non-linearity means that when two shock waves collide, they do not sum in the way that sound waves do – the collision of shock waves yields a higher pressure than the pressures of the individual shock waves.
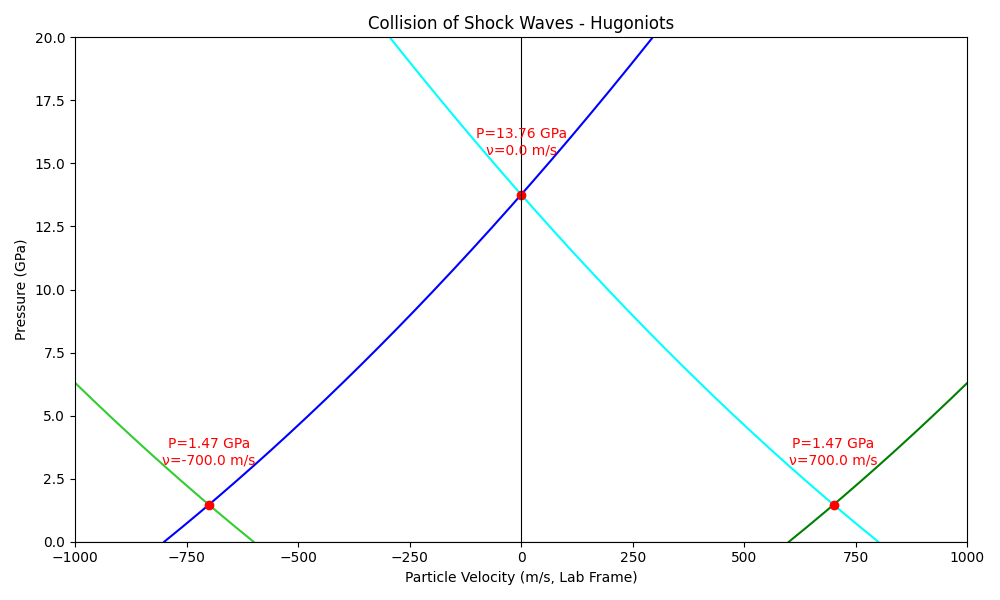
The idea that shock waves collide and result in a larger pressure than the sum of the individual pressures is the crucial point. If you want to understand a little bit more about why, the basic idea is that materials are shocked to points along a curve called a Hugoniot. The Hugoniot for a particular material describes the allowable states behind a shock wave so when two shock waves collide, their Hugoniot curves must intersect.
The figure below shows two shock wave Hugoniots (the ones going right are in blue, the ones going left are in green) and you can see that they intersect at a particle velocity of v = 0 with a huge pressure spike. This same concept applies to two shock waves of different particle velocities also, though the intersection will naturally shift.
This fact about shock wave collisions leads to an important tool in our tool kit: if we can use explosives in a carefully determined arrangement, we can shape the shock waves to collide in ways that will maximise our desired effect.
As we mentioned earlier, the effect that is going to be altered by creating higher pressure shock waves is the shattering effect. If we would like to shatter a material at a specific spot, wave shaping tools can be used to collide shock waves at that specific spot using much less explosive than would be required with bulk explosive techniques. All you need is a way of producing and transmitting shock waves so that they collide at a point or points of your choosing.
If before the way to increase the shattering effect was to add more explosive, now you have the opportunity to be more creative with how that explosive is used to create a disproportionate effect. What is important with waveshaping is that we configure the explosive train and initiation carefully in order to be confident where the shock waves will meet, and as part of that, use inert materials that area able to stop shock waves from travelling through the waveshaping material to disrupt the carefully configured explosive train. In other words, if we put a disc of wood in between two layers of sheet explosive but the wood is too thin for the thickness of sheet explosive, it is not inert enough as a waveshaper.
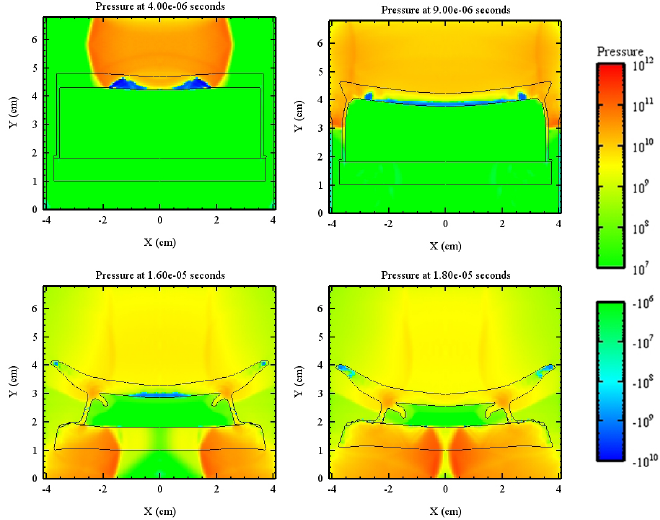
Perhaps the simplest model is one where an inert disc is used as in the figures below from DSTO (now DSTG) in Australia, and the shock waves converge to a point cylindrically at the bottom.
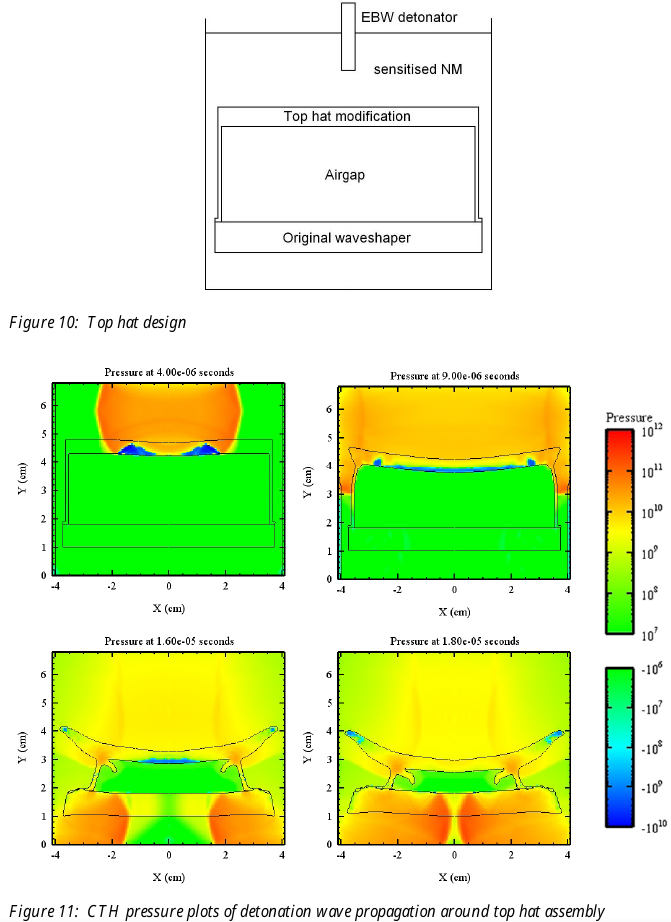
Other arrangements which generally conserve a “round” kind of symmetry allow for different convergence geometries, like converging on a disc. The important thing is that pressures far in excess of the detonation pressure of an explosive can be achieved by colliding shock waves. Just as importantly for military engineers, this can be achieved to a high standard under field conditions with readily available resources. You do not need your 3D shock waves to perfectly collide at a point to achieve an effective pressure multiplier from “near enough” collision.

Leave a Reply